Geometría Natural

Rubén Juárez López
Mnemosyne LLC.

Se puede argumentar que casi todas las formas de las geometrías con las que estamos familiarizados se encuentran en la naturaleza, pero esa noción desaparece fácilmente cuando incursionamos en campos más abstractos de la matemática. Aun cuando podemos argumentar que los artefactos de la matemática -por ser creaciones (descubrimientos?) de los humanos- son en sí parte de la naturaleza, limitaremos nuestra discusión al marco canónico de las “ciencias naturales” y su relación con las artes visuales.
La Arquitectura, las artes y la ciencia convergen en este dominio de manera perfectamente natural. De hecho, podemos decir que han estado inextricablemente unidas desde los albores de la civilización. Mucho antes de que Mandelbrot inventara la palabra “Fractal”, los conceptos de “Autosimilaridad y Propagación” y las matemáticas necesarias para describirlos habían avanzado por siglos. Muchos estudiosos de las plantas habían observado las regularidades de la serie de Fibonacci en las piñas y piñones, en el brócoli o el helecho. Antes de que la serie fuera introducida de manera formal- Estas regularidades han sido objeto de profundo estudio tanto en la matemática subyacente como en el hecho mismo. Los conceptos de la matemática necesarios son fácilmente asequibles a nuestra intuición sin tener que entrar a los detalles más profundos de su tejido.
Este libro existe en formato impreso y en formato digital. En todos los casos, recomendamos leer cada sección omitiendo los enlaces y, después, -en una segunda lectura-, acceder a los enlaces a la profundidad deseada. Esta advertencia es importante porque cada enlace nos abre nuevos caminos que no podemos recorrer en toda su plenitud. Esta es una de las mejores características del uso de la web, pero también, es necesario acotar su uso para poder sacar máximo provecho de esta lectura. En ediciones no digitales, esta circunstancia no existía como la presentamos, aunque el escritor perspicaz siempre sabía como dirigir al lector hacia las fuentes apropiadas. Lo único que cambia, es el mecanismo.
En unas partes del libro sugerimos usar software existente para experimentar o para visualizar algunos de los conceptos expuestos. En algunos casos, el software se usa para visualizaciones, pero en otros, se puede usar para manipular las visualizaciones y para crear otras nuevas. NetLogo es un ejemplo. Es un lenguaje de programación que nos permite crear nuestras propias visualizaciones, pero también tiene una biblioteca muy completa de modelos ya hechos que usaremos en este libro.
itp.uni-frankfurt.de/~gros/Vorlesungen/SO/simulation_example/
https://itp.uni-frankfurt.de/~gros/Vorlesungen/SO/simulation_example/
Una de las características fundamentales de la mente humana, es la de entender la idea de infinito; la idea de que siempre hay algo más grande que nosotros, de que no importa que tan lejos podemos ver, siempre hay más que ver.
No importa qué tanto podemos enumerar, siempre podemos extender la enumeración. No importa qué tanto podemos dividir un número real, siempre podemos seguir dividiéndolo.
En la cultura de occidente el concepto de infinito siempre ha causado inquietud. Zenón de Elea creó sus famosas paradojas en las que la lógica no coincidía con la realidad!
Para entender como Zenón entendía el infinito de lo muy pequeño, podemos hablar de la paradoja de la dicotomía: https://en.wikipedia.org/wiki/Zeno%27s_paradoxes#Dichotomy_paradox
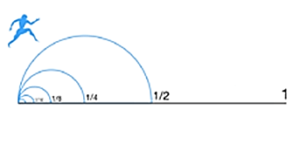
Supongamos que Atalanta desea correr hacia el final del camino. Antes de poder llegar, tiene que llegar a la mitad del camino, pero antes de llegar a la mitad, tiene que llegar a la cuarta parte. Antes de llegar a la cuarta parte, tiene que llegar a la octava parte… etc.
La dicotomía
El infinito de lo muy grande era más familiar porque la intuición de la serie de los números enteros es fácilmente adquirida. 1,2,3,4,5… hasta infinito
Lo mismo podemos decir de la serie de números primos 2,3,5,7,11,.. Son números solamente divisibles entre sí mismos. Este es otro ejemplo de series infinitas conocidas desde tiempos antiguos.
Una buena discusión sobre el infinito la podemos tener en la página de “Internet Encyclopedia of philosophy” https://iep.utm.edu/infinite/ y en el libro de David Foster Wallace “ Everything and more. A compact history of infinity” https://www.amazon.com/Everything-More-Compact-History-Infinity/dp/0393339289/ref=sr_1_14?crid=38O2FPL2NMZBD&dchild=1&keywords=david+foster+wallace&qid=1596615555&sprefix=david+fost%2Caps%2C212&sr=8-14
Un primer ejemplo del uso del infinito de lo pequeño que aplica a la geometría natural, lo podemos encontrar en el llamado “Polvo de Cantor”.
Este concepto resulta de iteraciones sucesivas de una “receta” simple:
- Dividir un segmento de recta en tres partes
- b) Cortar la segunda de estas tres partes
- c) A cada una de las partes resultantes, aplicar a y b
- d) Volver al paso a
![]()
Este procedimiento lo podemos aplicar tantas veces como queramos. Al mismo tiempo que cada “partícula de polvo” se hace más pequeña, el número de partículas se hace más grande. Los dos lados del infinito están presentes.
Al mismo tiempo que en el polvo de Cantor exploramos ambos extremos del infinito, aplicamos un procedimiento iterativo; es decir: aplicamos de manera repetitiva un procedimiento hasta un punto “práctico”. En el ejemplo de esta ilustración, hay siete iteraciones.
Una explicacion mas tecnica del polvo de Cantor la podemos encontrar en:
Habiendo entendido la lógica de la generación del polvo de Cantor, podemos extenderla de muchas formas. Comencemos por el copo de nieve de Koch.
Este fractal se genera con el procedimiento siguiente:
- En cada lado de un triángulo equilátero, remover la segunda tercera parte de cada lado
- Sobre el espacio dejado se coloca un triángulo equilátero con base ⅓ del triángulo anterior.
- Se elimina la base
- Volver al paso a
Presentamos las primeras cuatro iteraciones:
Si pensamos en una mesa (vista desde arriba), podemos ver que en la primera iteración podemos representar una mesa a la que se sientan 3 personas, en la segunda ya podemos acomodar a 12, en la tercera 48 y en la cuarta 192.
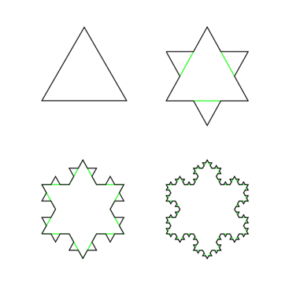
Nos resulta claro que podemos seguir iterando la generación de este fractal hasta el infinito… en la práctica esto significa que el perímetro del copo de nieve de Koch, es infinito mientras que el área dentro de la curva converge hacia 8/5 del área del triángulo original. Hacia la cuarta iteración, la mesa podría extenderse a un jardín muy amplio.
Lo interesante es que un polígono con área finita, tenga un perímetro infinito.
Este fractal tiene variaciones muy interesantes y se pueden ver en:
En el copo de nieve de Koch, nuestra atención estaba puesta en una curva cuya longitud se hacía infinita mientras que el área dentro de ella converge a un valor determinado.
La alfombra de Sierpinski nos ofrece algo que siendo similar en su lógica de producción, nos presenta posibilidades nuevas. La lógica de producción resulta clara; al añadir una nueva dimensión, la tercera parte que en la dimensión lineal define la geometría del polvo de cantor y del copo de nieve de Koch, sigue funcionando al agregar una nueva dimensión. En esta nueva realidad de dos dimensiones, el plano definido por un cuadrado regular, se divide en nueve partes. Extendiendo la lógica de producción de una dimensión, podemos ver que la primera iteración en dos dimensiones requiere que el cuadrado número 5 sea eliminado.
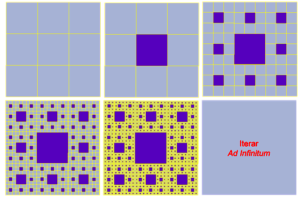
A primera vista podemos ver que a medida que iteramos el proceso de construcción, el área disminuye.
También podemos observar que la suma de los perímetros de los cuadrados internos tiende a infinito muy rápidamente (tan rápido como el área total de la superficie tiende a cero!
También podemos observar que en cada iteración, se producen diferentes anchos de superficies; en la primera iteración, tenemos el ancho de toda la superficie y el ancho de la tercera parte que se cortó. En la segunda iteración, se agregan no sólo el ancho de la nueva superficie cortada sino también la suma de las nuevas subdivisiones. En la segunda iteración, podemos ver anchos de dos unidades de superficie y así podemos continuar hasta el infinito…
En solamente unas pocas iteraciones, podemos apreciar una multiplicidad de usos:
Cuando comenzamos a usar teléfonos celulares usábamos antenas telescópicas para recibir la señal. Esas antenas, típicamente median entre diez y veinte centímetros y poco a poco se fueron reduciendo. En estas antenas, la longitud de la antena era determinante de la misma manera que lo es ahora. En la alfombra de Sierpinski, podemos apreciar cómo hay una cantidad enorme de longitudes con ancho específico. Una variación de la alfombra de Sierpinski seguramente está en un microcircuito que sirve como antena en virtud de poder captar frecuencias múltiples. Con un martillo debidamente aplicado a un teléfono celular moderno, podemos verificar esta aserción.
Hay muchas variaciones de la alfombra de Sierpinski que pueden comenzar a explorarse en https://en.wikipedia.org/wiki/Sierpinski_carpet
—–
Si por “Extrusión” proyectamos a la alfombra de sierpinski a una tercera dimensión, tendríamos un tubo cuyo perfil es cualquier iteración que queramos de la alfombra.

Otra manera de traer a la alfombra de Sierpinski a tres dimensiones, es el replicar sus reglas de producción en tres dimensiones como lo podemos ver en la “Esponja de Menger”
A primera vista la esponja de Menger nos muestra su origen en los fractales anteriores.
Inmediatamente podemos ver que las reglas de producción son similares a los anteriores:
- Comenzar con un cubo,
- Dividir cada cara del cubo en nueve partes (como en un cubo de Rubik)
- Remover el cubo menor en medio de cada fase, y remover el cubo menor del centro del cubo total. Lo cual nos deja 20 cubos menores. Esta es una esponja de Menger de nivel 1
- Repetir pasos 2 y 3 para cada uno de los cubos restantes y continuar iterando ad infinitum
La figura siguiente nos muestra las primeras cuatro iteraciones en la producción de la esponja de Menger.

Posiblemente algún arquitecto haya visualizado un centro de distribución o ciudades tridimensionales…
Los Químicos y los Industriales habrán visto superficies para catálisis y “cubos” de producción/distribución.
Los artistas… siempre lo han visto y expresado pero pocas veces explicado.
“La Biblioteca de Babel” de la historia de Jorge Luis Borges, pudiera ser consistente -Arquitectónicamente- con la esponja de Menger…
El universo (que otros llaman la Biblioteca) se compone de un número indefinido, y tal vez infinito, de galerías hexagonales, con vastos pozos de ventilación en el medio, cercados por barandas bajísimas. Desde cualquier hexágono se ven los pisos inferiores y superiores: interminablemente. La distribución de las galerías es invariable. (inicio de la historia…)
Aunque en principio es posible extruir o expandir dimensiones en la esponja de Menger, la visualización y realización material se dificultan sobre todo para quien no tiene orientación matemática.
Lo que podemos hacer de manera fácil es crear agregaciones con el expediente de conectar varias esponjas de Menger que incluso pueden tener variaciones dimensionales.
Podemos crear “retículas” que se pueden expandir en varias dimensiones. Podemos por también crear una “Rosca de Menger” mediante la agregación de esponjas de Menger cuyo plano superior se define por coordenadas polares en las caras externa e interna de la “rosca” con un origen arbitrario mientras que las otras dos dimensiones se mantienen con coordenadas cartesianas.
Una sección de tal rosca se puede ver en la segunda imagen y la constitución de la rosca sería una secuencia de esponjas modificadas con las curvaturas correspondientes.
Además de roscas, se podrían hacer gusanos…y redes de diversas formas.
Variaciones interesantes (y la mayor parte del contenido de esta sección, se pueden encontrar en
https://en.wikipedia.org/wiki/Menger_sponge

Este tipo de fractales es el más familiar y más fácil de visualizar.
En la generación de este fractal hay solamente dos variables fundamentales:
- El ángulo en el punto de la bifurcación y,
- La proporción en la que las ramas resultantes reducen su longitud respecto de la rama “precursora”
En la práctica, debemos de considerar un límite superior a las iteraciones porque en teoría podemos iterar hasta infinito. También habrá que considerar -casi siempre-, el ancho de las ramas.
En el árbol de este ejemplo el ángulo es de 30 grados y la relación de longitudes de rama precursora a rama actual es de ⅔.
- A partir de la base se construye un tronco de longitud L
- El tronco se bifurca con una separación de 30 grados entre las ramas nuevas
- Cada rama se expande hasta llegar a ⅔ de la longitud de la rama precursora
- Iterar hasta el límite superior (en este ejemplo, n=11)
este árbol después de 11 iteraciones tiene 1024 ramas terminales.
Este tipo de fractales es posiblemente el más reconocible y como los bosques nos muestran, uno de los más útiles.
Antes de ver los árboles en tres dimensiones, consideremos la arborescencia en dos dimensiones.
En el año 2086, al Arquitecto Covarrubias le comisionan una unidad habitacional que albergue a 1024 personas y que sea “Verde”. Recordando que no hay nada más verde que un árbol, el Arquitecto Covarrubias -con ayuda de sus amigos-, programa un cuadricóptero que usando un algoritmo de “visitación de árboles” marca sobre el terreno cada “nodo” del árbol. Como el terreno era plano, las marcas consisten de unas pequeñas “bombas” que al interrumpir su caída, sueltan un colorante fluorescente para facilitar su localización visual, y colocan en el piso un transpondedor y geo localizador que orientarán a la maquinaria semiautomática que es guiada por los algoritmos correctos, y, prepara terreno, excava canales de distribución, extruye las tuberías necesarias para transporte de fluidos de ida y vuelta así como también las redes eléctricas tanto de ida como de vuelta, etc. etc.
Arquitecto Covarrubias le comisionan una unidad habitacional que albergue a 1024 personas y que sea “Verde”. Recordando que no hay nada más verde que un árbol, el Arquitecto Covarrubias -con ayuda de sus amigos-, programa un cuadricóptero que usando un algoritmo de “visitación de árboles” marca sobre el terreno cada “nodo” del árbol. Como el terreno era plano, las marcas consisten de unas pequeñas “bombas” que al interrumpir su caída, sueltan un colorante fluorescente para facilitar su localización visual, y colocan en el piso un transpondedor y geo localizador que orientarán a la maquinaria semiautomática que es guiada por los algoritmos correctos, y, prepara terreno, excava canales de distribución, extruye las tuberías necesarias para transporte de fluidos de ida y vuelta así como también las redes eléctricas tanto de ida como de vuelta, etc. etc.
Como el diseño está basado en el fractal de árbol, todos los cálculos son algebraicamente similares (isomórficos)…
Excelente idea Sr. Covarrubias! Exclama el presidente del consejo de directores, pero en donde -y como- vamos a poner a las 1024 personas? Y no le parece que el diseño es demasiado “complicado”?Ah, comencemos por el principio: El diseño fractal inicial solamente se encarga de hacer eficientes todos los procesos de distribución y formación. Como podemos ver, después de once iteraciones, nuestro árbol tiene exactamente 1024 ramas externas!. Como el requerimiento es que diseñe algo para 1024 personas, a cada rama externa se le puede asignar un espacio de habitación individual que puede contener a su vez, varios subsistemas. En la ilustración siguiente, podemos ver uno de los extremos de la arborescencia que les mostré anteriormente. Aquí podemos apreciar las ramas terminales y si quieren contarlas en todo el árbol, podrán verificar que son exactamente 1024.

En cada una de las ramas terminales. Podemos erigir estructuras homeomórficas que nos producirán variedad de formas y funcionalidades sin sacrificar las funcionalidades de nuestra arborescencia. Podemos hacer espacios con forma de domos geodésicos, cilindros, prismas, espirales de fibonacci proyectadas en tres dimensiones…
Un momento señor Covarrubias! . – El presidente del consejo interrumpe la perorata del Arquitecto-. Hasta antes de los isomorfismos, homeomorfismos y espirales de Fibonacci íbamos muy bien!
Disculpe mi entusiasmo señor presidente…. La manera más fácil de explicar estas ideas, es conectarnos a la sesión de “Zoom” en la que Ruben Juarez está tratando de explicar estos conceptos…

Las espirales siempre han sido objeto de curiosidad y estudio. Su aparición como objetos geométricos es tan antigua como nuestras capacidades de representación. De hecho -como veremos más adelante,-, es aún más antigua….
Como por ahora nuestro tema son los fractales, nos concentramos en dos espirales que son ampliamente conocidas y usadas por artistas y arquitectos.
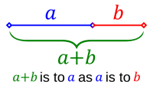
La espiral dorada se genera a partir de la “proporción áurea” :
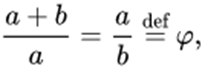
La espiral Dorada https://en.wikipedia.org/wiki/Golden_spiral
Es una espiral logarítmica cuyo factor de crecimiento es
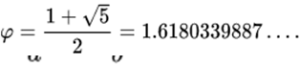
Citaré al artículo de Wikipedia :https://en.wikipedia.org/wiki/Golden_ratio
Esta relación define la proporción entre dos números cuya suma es proporcional al mayor de ellos de la misma manera que el mayor es al menor. es una solución de la ecuación x2-x=0
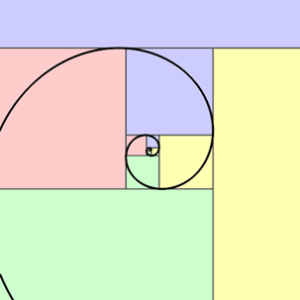
La espiral se ensancha cada cuarto de vuelta por un factor de φ
La espiral de Fibonacci, se genera a partir de la serie de Fibonacci: https://en.wikipedia.org/wiki/Fibonacci_number
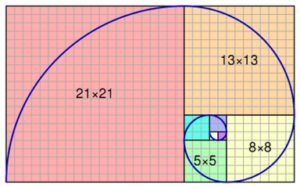
0 1 1 2 3 5 8 13 21..
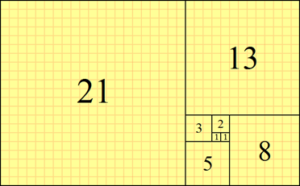



El artículo de wikipedia contiene descripciones y enlaces fascinantes acerca de la historia de esta serie que -naturalmente- comienza en la India.
[describir el art’iculo de prosodia sobre Pingala]
Por mor de tiempo nos concentramos en occidente;
Leonardo de Pisa, conocido como Fibonacci. En su libro Liber Abaci Publicado en 1202, Introdujo la secuencia a las matemáticas de Europa occidental. La serie : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …. Se forma sumando los dos elementos previos a cada elemento. La construcción de la espiral de Fibonacci se puede ver en los diagramas 1 y 2.
La instanciación de la espiral en formas naturales la podemos apreciar en las fotos de las plantas de sábila, de brócoli y en la concha del nautilo. La observación de periodicidades en las formas de la naturaleza es muy antigua y se ha dado en prácticamente todas las culturas.
El estudio matemático de las formas -en occidente-, es bastante más moderno. Se puede argumentar -con cierta razón- que Pitágoras y Arquímedes comenzaron tales estudios, pero en lo que toca a la matemática moderna, fue Descartes y después Jacob Bernoulli quienes iniciaron los estudios formales sobre las formas espirales. Este último hizo la observación de que la “espiral dorada” exhibía la propiedad de auto-similaridad, es decir, en cada cuarto de vuelta de la espiral, la curvatura es idéntica y el crecimiento es proporcional. Esta propiedad de la espiral fue lo que hizo que Bernoulli diera a la espiral dorada el nombre de “Spira Mirabilis”.
En relación a la biología, D’Arcy Thompson describe las espirales de los cuernos de rumiantes así como las conchas de moluscos como espirales logarítmicas y, describe la filotaxis y su relación con la serie de fibonacci. https://en.wikipedia.org/wiki/Phyllotaxis La palabra filotaxis denota “un arreglo de las hojas en torno a un tallo”
En este punto es que las arborescencias y las espirales se unen en tres dimensiones…
https://en.wikipedia.org/wiki/Golden_ratio
https://en.wikipedia.org/wiki/Golden_spiral
https://en.wikipedia.org/wiki/List_of_spirals
https://en.wikipedia.org/wiki/Patterns_in_nature
Señor Covarrubias, -interpelo el presidente del consejo-, Me encuentro en una situación un poco extraña; antes de conectarnos a la conversación con el Señor Juárez, no había entendido la mitad de todas las cosas que usted me dijo. Después de escuchar al señor Juárez, ya las entiendo, pero ahora no entiendo la mitad de todo lo que el señor Juárez está diciendo!!…
Ah! Vamos por buen camino respondió el Arquitecto Covarrubias…
Ahora que yo voy a continuar, se que entenderá cuando menos la mitad de lo que yo le diga además de lo que el señor Juárez dijo.
pero por lo pronto, aprovechando que ya me entendió lo que le dije antes de ir a ver la conversación, lo voy a platicar de como acomodaremos a 1024 personas en una estructura arborescente…
Entre las 1024 personas, habrá solter@s o familias de múltiples composiciones y extensiones…
Con un poco de ingenuidad y perspicacia, el diseño urbano se escribe solo!.
A partir de cierto nivel de “profundidad” en el árbol, se distribuyen las “unidades habitacionales” en función de su composición. Se asume que habrá migraciones, además de decesos y nuevas adiciones y, -por supuesto-, vacaciones….
Por mor de eficiencia, sigamos nuestra conversación hasta que ya no entienda la mitad de lo que le digo.
Parece ser que el método de volver a lo que Ruben Juarez está explicando, funciona bien cuando llegamos al punto en que usted ya comienza a no entenderme…
Si señor!.
Como le iba diciendo; para definir la ubicación de un@s nuev@s habitante(s), entenderemos al grupo que lo habitará, como función de la demografía local.
Consideremos como ejemplo a una familia de 5 a partir de la pareja que los origina. Esto quiere decir: progenitores más tres vástagos. En el diseño que le presento, hay dos maneras de acomodarlos: una es simplemente reservar un número de ramas exteriores para acomodarlos, la otra es usar también los nodos inmediatamente anteriores a las ramas. Esos detalles se pueden incluso decidir caso por caso…Comencemos por el diseño más simple, es decir; en el que a cada persona se le asigna una de las ramas exteriores del árbol que – después de todo-, tiene el número de ramas exacto para las 1024 personas y, si contamos los nacimientos y decesos a lo largo del tiempo, siempre puede haber ajustes.
Siendo las ramas terminales iguales en cuanto al grosor, podemos a;adir esrtructuras flexibles que extiendan su funcionalidad Por ejemplo, para una familia de 6 personas, se pueden distribuir seis de las ramas terminales hacia una unidad habitable de la forma que se desee.
Ahora que hemos visto la lectura del señor Juárez, podemos entender lo que son los homeomorfismos y como podemos aplicar tal concepto: Comencemos por recordar que los isomorfismos entre las ecuaciones que definen a los fractales son “similaridades” algebraicas…
“Creo que eso ya lo tengo claro” exclamó el presidente…Muy bien -dijo el Arquitecto-, ahora debemos de explicar que los homeomorfismos, se refieren a similaridades “Topológicas…”
“Topo what?!!!” exclamó el presidente con tono ligeramente exasperado…
¿Qué le parecen las donas que nos estamos comiendo con el café?
Están deliciosas, me gustan más que las de “Krispy-Kreme”, ¡pero no me cambie la conversación!
No la estoy cambiando, -respondió el Arquitecto al tiempo que sacaba de la bolsa interior de su saco una dona de plastilina a la que transformó en una taza de la manera siguiente:
–![]()
Como puede ver, el agujero de la dona es ahora el asa de la taza y, el cuenco de la taza se forma sin crear agujeros nuevos!. Es decir, cada punto en la plastilina sigue guardando la misma relación con sus puntos vecinos! La taza y la dona son homeomorfas porque la deformación elástica que hace que una se convierta en la otra, preserva intactas todas las relaciones.
La topología es una geometría en la que las relaciones entre puntos son más importantes que su posición en un sistema de coordenadas.
Creo que ya comprendo lo que me trataba de explicar antes acerca de las unidades homeomórficas…
Si! Interpela el Arquitecto al mismo tiempo que resume la perorata del capítulo anterior…
La familia de Rapunzel insistió en una serie de torres cilíndricas mientras que los Buckminster-Fuller ‘s querían domos geodésicos. El profesor Juárez, quiso un grupo de unidades no muy diferentes a la mezquita de Santa Sofía…el módulo central, tiene un domo con las proporciones exactas y junto con las paredes, proporciona el espacio apropiado para sesiones de multimedia simplemente espectaculares.
Los minaretes, contienen laboratorios para diversos fines. En uno de ellos se estudia la “Temptónica” (Ciencia de las tentaciones), en otro -conectado al primero por galerías subterráneas-, se estudia la “Ferolingüística” (algo relacionado con comunicación y Feromonas…)… de lo que pasa en los otros dos minaretes, solamente le puedo decir lo que podrá leer en el apéndice 9 del libro que Ruben y yo estamos escribiendo del cual le traje una copia a regalar….
Un momento señor!. Me está usted tomando el pelo?
Como que lo están escribiendo y ya me está entregando una copia ya terminada?
Er… Permítame explicar… todo esto es a causa de MITO…
¿Qué es eso? !!
Ah, MITO es un acrónimo del Módulo Individual de Transporte Orgánico…
Antes de explicar qué es MITO y como tiene relevancia a mi situación actual, puede ser bueno ver un poco más de la lectura del profesor Juárez…
Lo que encuentro un poco extraño es que en la lectura que está teniendo lugar en 2020, aparezco en la sesión de “Zoom” aun cuando yo estoy aquí con usted en el año 2086?.
Ah, en uno de los otros minaretes de la mansión se hacen experimentos con el tiempo,
pero esa es otra historia…
Autosimilaridad estadística y dimensión fraccional.
Este fue el título de un papel de Bennoit Mandelbrot en el que introdujo por primera vez la idea de “Fractal” en 1967. El término lo inventó en 1975.
Una paradoja curiosa es que la respuesta depende de la longitud de la medida usada; si usamos una “vara” de 200 kilómetros de longitud, la costa mide 2400 kilómetros. Si usamos una vara de 50 kilómetros, la longitud será de 3400 y así sucesivamente… Las siguientes imágenes ilustran la idea…
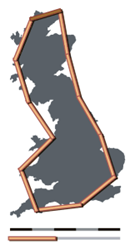
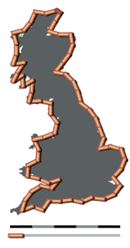
En este trabajo, Mandelbrot hace énfasis en que medir la longitud de una costa es un ejercicio relativamente complicado. Usando una ecuación empírica desarrollada por Lewis Fry Richardson, Si la costa es relativamente suave y homogénea ‘como la costa de África del sur, la “dimension” de la costa se aproxima a 1.02 mientras que la costa del oeste de Inglaterra, tendría una dimensionalidad de 1.25. La “dimensionalidad” es un número mayor que 1 y menor que 2.
https://en.wikipedia.org/wiki/Hausdorff_dimension
El conjunto de Mandelbrot
El conjunto de mandelbrot está formado por los números complejos para los cuales la función no diverge cuando se itera desde z=0….

Este conjunto ha sido explorado de diversas maneras y existe software de bajo costo que hace posible su exploración en cualquier computadora de escritorio.
Los fractales mostrados en este trabajo, fueron generados con el software Fractal Extreme by Cygnus Software.
Newton fractal – Wikipedia (z,z3%20%E2%88%92%202z%20%2B%202.
El atractor de Lorenz, a menudo denominado mariposa de Lorenz, es un objeto matemático que surge de un conjunto de ecuaciones diferenciales conocidas como ecuaciones de Lorenz. Fue estudiado por primera vez por el meteorólogo y matemático estadounidense Edward Lorenz a principios de la década de 1960, mientras investigaba la convección atmosférica, concretamente la predicción del tiempo.
El atractor de Lorenz es un sistema dinámico caótico tridimensional, y sus ecuaciones vienen dadas por:
dx/dt = σ(y – x) dy/dt = ρx – y – xz dz/dt = xy – βz
Aquí, x, y y z representan las variables de estado del sistema, y σ, ρ y β son parámetros. Estas ecuaciones describen el comportamiento de un modelo simplificado de convección atmosférica, en el que x representa la velocidad de convección, y representa la diferencia de temperatura entre las corrientes de aire ascendente y descendente, y z representa la distribución de la temperatura en la atmósfera.
El atractor de Lorenz es famoso por su comportamiento caótico e impredecible, aunque las ecuaciones subyacentes sean deterministas. Cuando se simula o se representa en un espacio tridimensional, tiene una forma característica que recuerda a una mariposa o a un par de alas. Esta forma demuestra la sensibilidad de los sistemas caóticos a las condiciones iniciales, un fenómeno descrito a menudo como el “efecto mariposa”, en el que pequeños cambios en las condiciones iniciales pueden conducir a resultados drásticamente diferentes con el tiempo.
El atractor de Lorenz tiene aplicaciones que van más allá de la meteorología y la predicción del tiempo. Se ha estudiado en los campos de la teoría del caos, la dinámica no lineal y las matemáticas, y es un ejemplo clásico de sistema caótico con profundas implicaciones para comprender los comportamientos complejos e impredecibles de diversos sistemas naturales y artificiales.
https://itp.uni-frankfurt.de/~gros/Vorlesungen/SO/simulation_example/

La catenaria es la curva que describe una cadena que estando sujeta en sus dos extremos, cuelga libremente. La fuerza de la gravedad, da una forma única que, si se invierte, nos presenta la distribución de fuerzas opuestas a la gravedad.

In 1671, Hooke announced to the Royal Society that he had solved the problem of the optimal shape of an arch, and in 1675 published an encrypted solution as a Latin anagram[16] in an appendix to his Description of Helioscopes,[17] where he wrote that he had found “a true mathematical and mechanical form of all manner of Arches for Building.” He did not publish the solution to this anagram[18] in his lifetime, but in 1705 his executor provided it as ut pendet continuum flexile, sic stabit contiguum rigidum inversum, meaning “As hangs a flexible cable so, inverted, stand the touching pieces of an arch.”
Wikipedia
En 1671, Hooke anunció a la Royal Society que había resuelto el problema de la forma óptima de un arco, y en 1675 publicó una solución cifrada como un anagrama en latín[16] en un apéndice de su Descripción de los Helioscopios,[17] donde escribió que había encontrado “una verdadera forma matemática y mecánica de todo tipo de Arcos para la Construcción.” No publicó la solución a este anagrama[18] en vida, pero en 1705 su albacea la proporcionó como ut pendet continuum flexile, sic stabit contiguum rigidum inversum, que significa “Como cuelga un cable flexible así, invertidas, están las piezas que se tocan de un arco.” Wikipedia
Pero,… eso ya lo sabían las termitas, y los arquitectos pronto aprendieron los beneficios de su uso.



Una buena descripción de la matemática la podemos encontrar en Wikipedia
https://es.wikipedia.org/wiki/Catenaria
El autómata celular (AC) es un modelo computacional discreto que consiste en una rejilla de celdas, cada una de las cuales puede estar en uno de un número finito de estados. Se trata de un concepto sencillo pero potente que se utiliza en diversos campos, como las matemáticas, la informática, la física y la biología. Los autómatas celulares se utilizan para estudiar sistemas complejos y dinámicos, que a menudo muestran un comportamiento emergente a partir de reglas locales sencillas.
Entre las principales características de los autómatas celulares se incluyen
- Rejilla: El AC suele representarse como una cuadrícula bidimensional de celdas, aunque también puede extenderse a dimensiones superiores.
- Estados: Cada celda de la rejilla puede tener uno de un conjunto finito de estados posibles. Estos estados pueden representar diversas propiedades o condiciones del sistema modelado.
- Vecindad: Cada celda tiene una vecindad definida, que consiste en las celdas que la rodean. La vecindad puede definirse de diferentes maneras, como la vecindad de Moore (que incluye las ocho celdas adyacentes) o la vecindad de von Neumann (que incluye sólo las cuatro celdas ortogonalmente adyacentes).
- Pasos temporales: La AC evoluciona a lo largo de pasos temporales discretos. En cada paso temporal, el estado de cada célula se actualiza en función de un conjunto de reglas, que suelen incluir los estados de sus células vecinas.
- Reglas de transición: El comportamiento del autómata celular viene determinado por un conjunto de reglas de transición, que especifican cómo debe cambiar el estado de cada celda en función del estado actual de la celda y de sus vecinas. Estas reglas suelen expresarse mediante lógica booleana o tablas de consulta.
- Configuración inicial: El AC comienza con una configuración inicial, que especifica los estados iniciales de todas las celdas de la red.
Uno de los autómatas celulares más famosos es el Juego de la Vida de Conway, inventado por el matemático John Conway en 1970. En este AC, cada célula puede estar en uno de dos estados, “viva” o “muerta”, y el estado de cada célula evoluciona con el tiempo en función de un conjunto de reglas relacionadas con sus células vecinas. El Juego de la Vida de Conway se ha estudiado ampliamente y ha permitido descubrir diversos patrones y fenómenos interesantes.
Una buena introducción al juego de la vida, la podemos ver en Wikipedia https://es.wikipedia.org/wiki/Juego_de_la_vida. En la sección de taller, podemos experimentar con el software NetLogo y poder ver de primera mano cómo funcionan estos autómatas.
Los autómatas celulares tienen aplicaciones en diversos campos, como la modelización de sistemas físicos, la simulación de procesos biológicos, la generación de números aleatorios y el estudio del comportamiento emergente en sistemas complejos. También se utilizan en informática para la computación paralela y en criptografía para generar números pseudoaleatorios.

Ingredientes
- Masa para pizza
- Dos rebanadas de queso suizo, havarti, cheddar, o cualquier otro queso fundible que venga en rebanadas.
- Vegetales o carnes frías en rebanadas finas y yerbas colorantes molidas de manera fina
- Aceites coloreados con chile o con albahaca o con azafrán
- Cuerda de cocina, pinceles y papel de repostero
Preparación
En una mesa de panadero debidamente engrasada y enharinada se extiende masa de piza sobre una superficie de papel de cocina debidamente marcado con una retícula 3 x 3 tomando como unidad una rebanada del queso que estemos usando. Si la rebanada mide 10 centímetros, la reticula medirá 30 cm por lado
Una vez extendida la masa, se dibuja la retícula usando cuerda mojada en aceite de azafrán. Esta nueva retícula, tendrá subdivisiones adicionales después de una iteración extra

En el centro se coloca una rebanada de queso rodeada de manera proporcional de ocho de las nueve subdivisiones hechas a la secunda rebanada con un cortador de pizza
Con otra rebanada de queso cortada en nueve partes, a su vez divididas por nueve nos resulta en
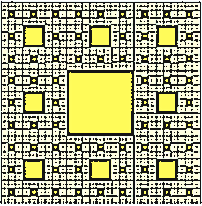
En este punto, podemos aplicar aceites coloreados sobre la masa usando un pincel.
Sobre los quesos, se pueden espolvorear hierbas secas o frescas finamente divididas y sobre la masa, confeti de frutas, vegetales o proteína crujiente.
Sobre una superficie plana de dos metros por uno, dibujar un sistema circulatorio como el que se muestra
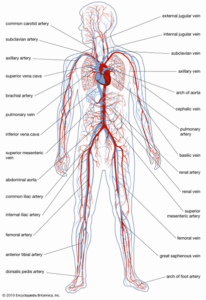
Con una máquina de hacer pasta, preparar el doble de la pasta necesaria para con diferentes diámetros de pasta.
cubrir el dibujo de tal manera que la pasta quede del grosor de las arterias, venas, y vasos capilares.
Esto se hace con la pasta sin cocinar. Se puede colorear la pasta con polvo de chile, o cualquier otra yerba colorante. Es importante mantener la comestibilidad de los materiales. Una vez que se tiene el modelo terminado, se estabiliza dimensionalmente y se pone en una mesa separada.

Se toma la otra mitad de los fideos y se cocinan tomando nota del tiempo necesario para que queden al dente. Este tiempo variará en función del grosor del fideo, y hay que encontrar el tiempo óptimo para el resultado deseado.
Una vez logrado el resultado satisfactorio, se mide la longitud y el diámetro de los fideos resultantes y se tabulan al lado de las dimensiones de sus símiles no cocinados. Estos resultados habrán de discutirse después para facilitar la preparación de un banquete con los materiales cocinados.
Haciendo ajustes por los cambios de dimensiones, se reconstruye el sistema circulatorio sobre una mesa de panadero, limpia, y aceitada. Se le cubre con una capa ligera de salsa de tomate que fué preparada por separado con una receta favorita. Se colocan alrededor de la pasta, vegetales picados en grados de finura que hagan visualmente atractivo el platillo. Se rocía con vinagre balsámico y se espolvorea con quesos secos como pecorino, Romano, Parmesano etc. en moderación.
El corazón se puede construir con vegetales hervidos inspirados por las pinturas de Arcimboldo.

El corazón se puede construir con vegetales hervidos inspirados por las pinturas de Arcimboldo.
El corazón se puede labrar con betabeles, Alcachofas, zanahorias, etc.
El órden y el método en el que el plato final se consuma, son importantes y se debe de seguir usando los instrumentos apropiados.
El instructor, dirige al grupo al tiempo que explica el orden del procedimiento y la razón de ser así.
El evento, puede variar en la medida que se perfecciona.
Al concluir la cena, se sirven los postres que deberán de ser inspirados por la misma geometría.
Nota práctica. Por necesidades de operación, habrá que dividir la cocción de los vasos capilares respecto de las arterias y venas.
Seguramente los sistemas de irrigación agrícola modernos usan variaciones de esta extrusión… .Muchos sistemas de raíces en vegetales siguen configuraciones similares aunque, debido a variaciones ambientales las variaciones son enormes.
Este es un tópico interesante en el campo de la morfogenética con aplicaciones al quehacer humano.